Matrices and Camera Pose Estimation

• Thu, Apr 7, 2022
• 3-minute read
• Subscribe

Camera pose estimation

One of the essential features of Ace Trace app (a video editor) is to figure the camera motion as well as zoom changes.

This enables the app to pin an object trajectory to a certain point in the physical world coordinate system vs working in the camera viewport.

The process of estimation of the camera pose is called SLAM (Simultaneous Localization And Mapping), and here we’re are going to talk specifically about Visual SLAM, meaning that we’re only using the visual information to estimate the camera pose.

I’m going to show you how matrix transformations can be used in this process.

Let’s talk about matrix transformations

It’s not a secret you can use simple linear algebra to manipulate images, and layers, place objects into a 3D scene, and so on. I’m not going to explain the math behind it, there is an unlimited amount of information on the internet already. Look at this playground, I like their visualization, it’s super easy to understand how transformations work:

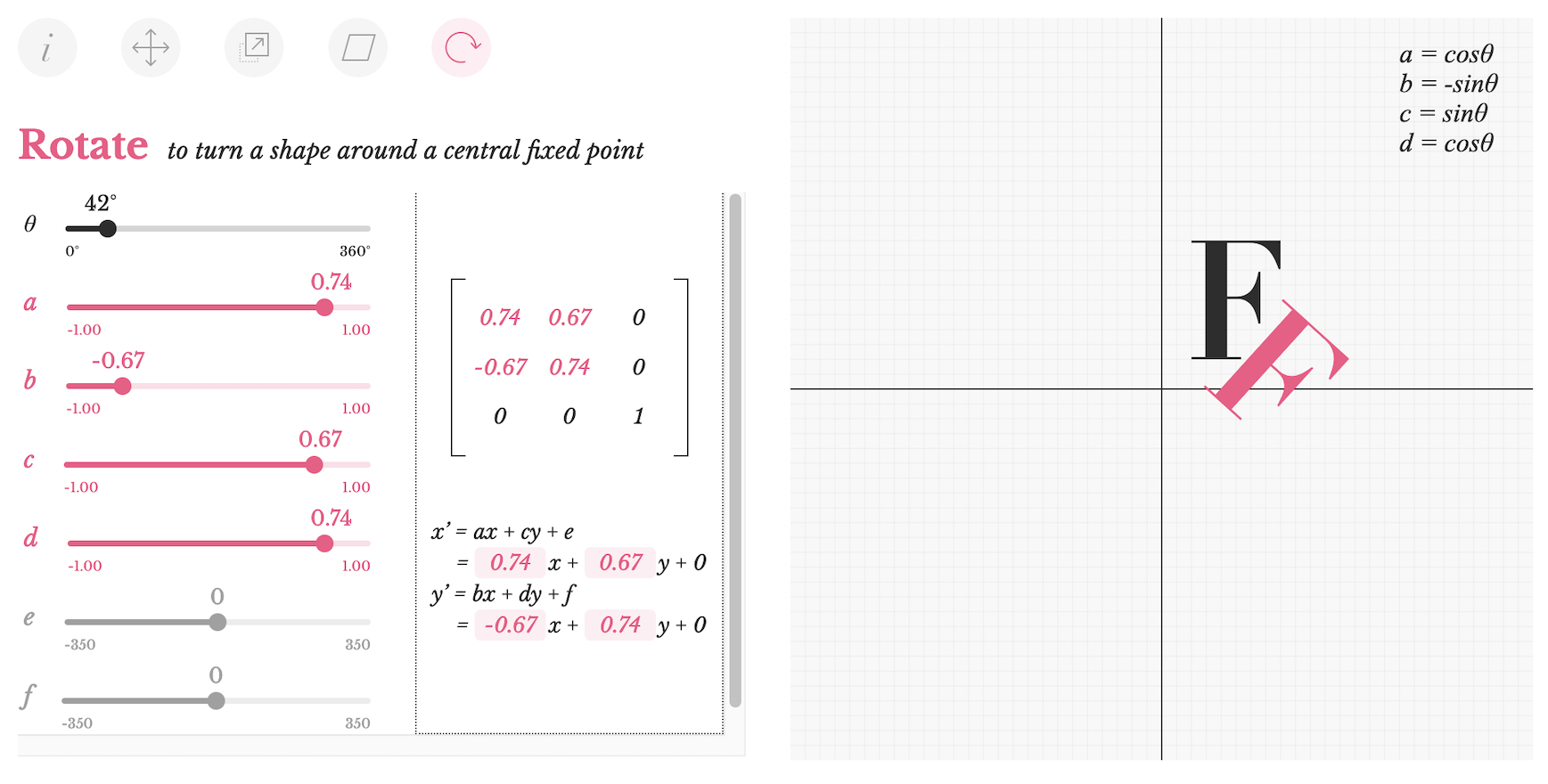
It’s worth adopting this mindset: every time you want to move or rotate something, you should use matrix transformations. Any standard library normally includes tools to execute matrix operations, and some APIs are only talking matrices - when it comes to GPU computing, it’s much more efficient, and everything in the 3D world is built around matrices. So go learn matrix algebra if you haven’t already!

The Visual SLAM algorithm performance issues

Running matrix operations using OpenCV will normally involve a lot of computation on CPU. It will perform poorly on mobile devices, especially when processing high-definition images. The simplest way to boost the performance is to downscale the image to a lower resolution, find the transformation, and then apply that matrix to the original frames.
Downscaling is pretty straightforward - just use something like resize function from OpenCV, which works pretty fast, allowing us to focus on the real issue here - finding the transformation matrix. And this part is very sensitive to the image resolution.
However, even after you found your downscaled transformation between frames, to properly apply these matrices you will have to prepare them to work for bigger images.

Apply downscaled transformations

Let’s say the original image is 1920x1080, and you want to downscale it to 640x480.

scale = 640 / 1920

Now given your downscaled transformation matrix, you can upscale it like this:

upscaled = scaleMatrix(scale) x downscaled x scaleMatrix(1/scale)

where x is the matrix multiplication operator.

1. We convert the coordinate system to the downscaled one first by using a scale transform scaleMatrix(scale).
2. Then we apply our downscaled transform.
3. We convert back to the original coordinate system by using this scale transform scaleMatrix(1/scale).

This way we make sure we apply our transform in the correct coordinate system.
In Swift language it looks like this:

let upscaled = CGAffineTransform(scaleX: scale, y: scale)
    .concatenating(downscaled)
    .concatenating(CGAffineTransform(scaleX: 1/scale, y: 1/scale))

The order of these operations is extremely important. I’ve spent some time before figuring out what is the matrix operation order under the hood. For example, one could use scaledBy or translateBy functions instead of concatenating to achieve the same result, however, they apply matrix multiplications in the reverse order. Always check the docs to make sure.

Conclusion

This way you can significantly boost the performance of your SLAM algorithm while keeping adequate quality. In my case, I’ve reduced the processing time from 1 minute to 20 seconds for 4K videos and to 7 seconds for 1080p, which is a huge improvement.
If you have Oculus Quest you probably noticed, how it tracks the pose of the headset in real time with insane accuracy. Even though they utilize the advantage of having accelerometer sensor data, they definitely excel at tracking algorithms and performance optimizations such as this simple approach.